
Présentation du problème
On fait tous des erreurs, on le sait. Et bien sûr, on n’aime pas ça.
C’est pourquoi, quand on mesure quelque chose, on ne fait pas qu’une seule mesure : on en fait plusieurs, pour s’assurer que l’on n’a pas fait d’erreur. C’est là que ça se complique, parce qu’en général on obtient des résultats différents à chaque mesure. Par conséquent, si on a bien la certitude qu’on s’est trompé, on ne sait pas où… Et on ne sait donc pas quelle est la bonne mesure (si tant est qu’on l’ait obtenue). Au final, on se dit que c’est à peu près bon, et que ce sera largement suffisant. C’est souvent le cas… Mais pas tout le temps.
Il arrive aussi, bien souvent, que le phénomène auquel on s’intéresse, et que l’on veut mesurer, ne soit pas unique, mais composé d’une multitude d’occurrences. Par conséquent, le mesurer une seule fois ne peut pas être représentatif de sa diversité. C’est le cas, par exemple, du temps passé sur une page web, qui varie d’une session à l’autre.
Qu’est-ce qu’une mesure ?
Selon Anne Myers et Christine Hansen :
« Mesurer consiste à attribuer une valeur numérique à des objets, des évènements ou à certaines de leurs caractéristiques selon des règles conventionnelles. »
Pour Maurice Reuchlin, mesurer consiste à :
« établir une correspondance entre certaines propriétés des choses et certaines propriétés des nombres. S’il l’on y parvient, on peut prévoir, en ce qui concerne ces propriétés, le résultat d’une opération effectuée sur des choses à partir d’une opération réalisée, de façon beaucoup moins coûteuse, sur des nombres. »
Cette dernière considération est fort utile, car elle peut permettre, sinon d’empêcher, tout du moins d’estimer notre risque d’erreur (notamment grâce à l’étude des probabilités, dont nous traiterons prochainement). Il existe plusieurs sources d’aléas (ou d’erreurs) au cours d’un mesurage (terme consacré pour l’action de mesurer) :
- Techniques (absence ou mauvais enregistrement de tout ou partie des données),
- Observation (on ne voit que ce qu’on veut bien voir, et aussi bête que cela puisse paraitre, la situation d’observation est autant de facteurs d’altération de la mesure),
- Mesure (précision et sensibilité),
- Échantillonnage (choix des mesures).
L’erreur de mesure
L’erreur de mesure a deux composantes :
- Une composante systématique, c’est-à-dire qu’on la retrouve dans chaque mesure, toujours de la même ampleur ou proportion. Elle est le plus souvent lié à l’étalonnage ou au fonctionnement de l’outil de mesure. Avec un peu de rigueur et de méthode, on peut (presque) facilement réduire l’erreur systématique à (presque) zéro.
- Une composante aléatoire, qui est, comme son nom l’indique, liée au hasard, et varie de façon « imprévisible ». Elle est la conséquence d’un ensemble de facteurs qui font que la mesure sera parfois supérieure ou inférieure à la valeur réelle, dans de faibles proportions (le plus souvent), et différentes à chaque fois.
L’illustration ci-dessous montre comment, en fonction de la valeur cible (ou vraie) que l’on veut mesurer (et qui peut être connue ou inconnue), on peut obtenir une valeur qui s’en écarte, plus ou moins, en fonction des effets combinés des erreurs systématique et aléatoire.

Exemple : temps de chargement de UXMetric.com
La mesure du temps de chargement d’une page web, par exemple, dépend de cela. Si l’on mesure 9 fois le temps de chargement d’uxmetric.com avec l’outil webpagetest.org, on obtient les résultats suivants :
| Mesures | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Durée (s.) | 0,731 s. | 0,739 s. | 0,760 s. | 0,747 s. | 0,820 s. | 0,784 s. | 0,823 s. | 0,725 s. | 0,735 s. |
Tab. 1 : Mesures du temps de chargement d’UXMetric.com
C’est dans un mouchoir de poche, certes, mais c’est différent à chaque fois, et jusqu’au 1/10ème de seconde. Notez que l’erreur aléatoire est très dépendante de la sensibilité de l’outil de mesure. Les mêmes durées ci-dessus, arrondies à la seconde, deviendraient rigoureusement identiques…
Vous pourriez objecter qu’il est normal pour la mesure d’un temps de chargement d’avoir des résultats si disparates : la demande en download et upload variant en permanence sur le réseau, il est normal que cela impacte constamment le temps de chargement d’une page. Mais si nous avions mesuré la longueur d’un clou avec un outil suffisamment précis, nous aurions obtenu les mêmes résultats : en fonction de la température ambiante, de celle des doigts du manipulateur, le métal du clou se dilaterait de façon différente à chaque mesure, de quelques microns en plus ou en moins à chaque fois, produisant ainsi des mesures différentes. Les conditions de mesure changent à chaque nouvelle mesure, même avec les plus grandes précautions.
Dans ces résultats, on sait donc qu’il y a des erreurs, mais on ne sait pas où, combien, ni dans quelle proportion. On ne sait pas plus quelles en sont les composantes systématiques et aléatoires. En partant du principe (certes arbitraire) que l’outil de webpagetest.org est bien calibré, on considère que l’erreur systématique est négligeable (nulle ou presque).
Reste l’erreur aléatoire. Si cette erreur est aléatoirement supérieure et inférieure à la valeur réelle (potentiellement inconnue), alors en faisant la moyenne des mesures obtenues, on devrait s’approcher de la valeur cible. C’est une bonne idée, mais c’est sans compter l’erreur d’échantillonnage.
L’erreur d’échantillonnage
Nous avons réalisé 9 mesures du temps de chargement d’une page web, mais rien ne nous permet de penser qu’elles sont représentatives de la totalité des mesures possibles, qui est potentiellement infinie. En effet, ces mesures ont été réalisées à un moment donné, avec un certain matériel et dans certaines conditions. Qu’est-ce qui nous ferait penser que les résultats ne seraient pas différents à un autre instant et dans d’autres conditions ? Rien…
C’est tout l’enjeu de l’échantillonnage : puisqu’il n’est pas possible (humainement, techniquement, financièrement) de faire TOUTES les mesures (ce qui est parfois possible, cela s’appelle un recensement), alors on ne va faire les mesures que sur un échantillon prélevé aléatoirement (sans quoi on introduirait un biais de sélection) parmi la population parente (c’est-à-dire l’ensemble des occurrences du phénomène étudié). Avec toujours le même problème : cet échantillon est-t-il représentatif de l’ensemble dans lequel il a été choisi ?
Un échantillon est un sous-ensemble d’une population-cible. Quand il a été prélevé aléatoirement ou de manière probabiliste, on peut penser qu’il est représentatif de la population. Cependant, même quand des échantillons sont numériquement importants, on ne peut pas présumer qu’ils soient en tous points conformes à la population-cible quant aux proportions des différentes catégories. Denis Poinsot illustre cela de la façon suivante dans son excellent (gratuit et en ligne) « statistiques pour statophobes » : deux échantillons forts différents peuvent être prélevés dans un même ensemble (cf. figure 2).
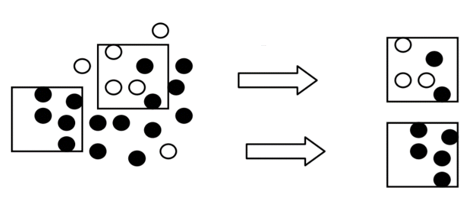
Ici, il s’agit d’un ensemble de boules noires et blanches, mais ce pourrait être « supérieur » ou « inférieur » à la valeur cible. La plus grande quantité de boules noires correspondant à une erreur systématique positive, par exemple. Ou à plus de femmes que d’hommes par exemple.
Exemple : parts d’hommes et de femmes parmi les lecteurs d’UXMetric
Justement, examinons la proportion d’hommes et de femmes qui consultent UXMetric.com à différentes périodes proches les unes des autres (d’après un jeu de données échantillonné, entre 24 et 39% des sessions, fourni par Google Analytics).
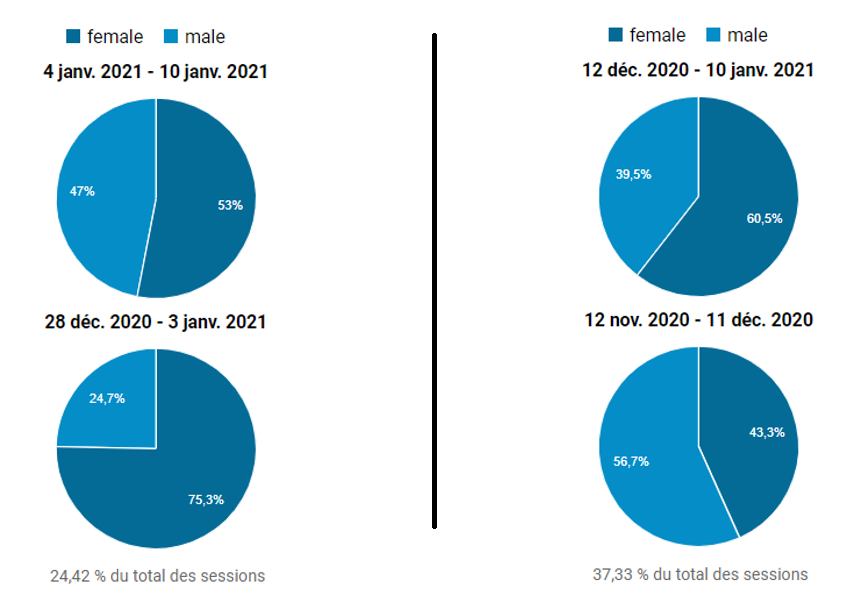
On constate que d’une semaine à l’autre (partie gauche de la figure 2), ce qui représente à peu près 130 utilisateurs hebdomadaires, la proportion hommes/femmes peut varier de façon importante. Sur une période plus longue (un mois, partie droite de la figure 2), pour à peu près 1200 utilisateurs mensuels, les différences persistent, mais s’estompent. Plus intéressant, on entrevoit que la moyenne des deux pourrait correspondre à un partage équitable des sessions entre hommes et femmes.
C’est ce que nous confirme l’examen des données démographiques par sexe depuis les débuts d’UXMetric.com, soit avril 2018 (cf. figure 3, soit à peu près 20 000 sessions) :
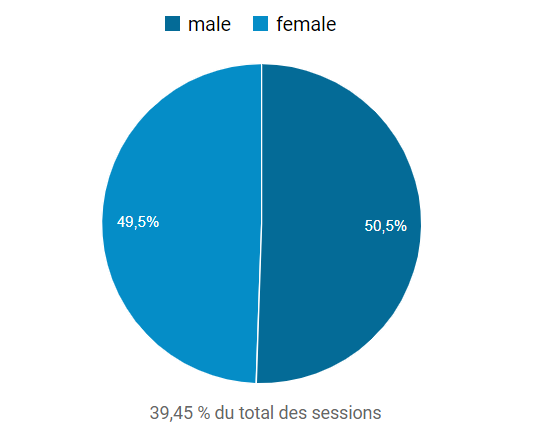
Cet exemple illustre donc à quel point l’échantillonnage, y compris pour des tailles relativement importantes (jusqu’à 1200 utilisateurs mensuels), peut fournir des résultats erronés. Ceux-ci vont donc ajouter de l’erreur d’échantillonnage à l’erreur de mesure existant par le fait même de mesurer. Dès lors, comment être sûr (ou presque) que des mesures sont suffisamment justes et représentatives du phénomène étudié ? Si l’on ne peut en avoir la certitude, peut-on connaitre notre risque d’erreur ?
Conclusion
La précision de l’évaluation d’un phénomène dépend à la fois des erreurs de mesure et d’échantillonnage. Ces deux types d’erreurs ont en commun d’être aléatoires, c’est-à-dire liées au hasard. Les probabilités sont la branche des mathématiques consacrée à la modélisation des phénomènes aléatoires. C’est pourquoi en avoir une compréhension minimale est indispensable à un bon usage des outils de mesures et des statistiques.
