
Mesure et hasard
Nous l’avons montré précédemment, la précision de l’évaluation d’un phénomène dépend à la fois des erreurs de mesure et d’échantillonnage. Ces deux types d’erreurs ont en commun d’être aléatoires, c’est-à-dire liées au hasard. C’est valable aussi bien en recherche utilisateur qu’en mesure de la performance digitale.
On se fait en général une idée assez fausse du hasard : on l’associe à une forme de chaos. Si c’est vrai pour de petits échantillons, le hasard devient en réalité très “organisé” dès lors qu’on multiplie les observations.
Qu’est-ce que le hasard ?
Antoine Augustin Cournot donne du hasard la définition suivante :
« Le hasard n’est pas que l’expression de notre ignorance des causes, c’est la rencontre de deux séries causales indépendantes. Les événements en eux-mêmes sont tout à fait déterminés quant à leur cause et à leur effet ; c’est de leur rencontre imprévisible, de l’intrusion d’une nouvelle causalité indépendante dans le déroulement d’un processus que naît le hasard. »
Les probabilités sont la branche des mathématiques consacrée à la modélisation des phénomènes aléatoires. En avoir une compréhension minimale est indispensable à un bon usage des outils de mesures et des statistiques.
En effet, lorsque l’on mesure une grandeur qui peut prendre différentes valeurs du fait du hasard, on dit qu’elle est aléatoire. Ainsi, les différentes valeurs qu’elle peut prendre sont dues à des causes, non pas nécessairement inconnues, mais dont la conjonction va avoir un effet sur elle que l’on ne peut pas prévoir. On dit ainsi que la variable se « distribue » sur les différentes valeurs (ou modalités) qu’elle peut prendre. La compréhension des variables aléatoires est intimement liée à celle des échelles de mesure.
Back to basics : le pile ou face
La base des probabilités, c’est le pile ou face (ou épreuve de Bernoulli en jargon mathématique) : on lance une pièce, et il y a une chance sur deux qu’elle tombe sur l’une ou l’autre de ses faces (si elle est équilibrée). C’est exactement la même chose que tirer au hasard une boule dans un sac qui en contient à chaque fois autant de noires que de blanches (c’est ce que l’on appelle un tirage avec remise : on remet la boule précédemment tirée dans le sac. Ainsi, le tirage suivant n’est pas influencé par le précédent, ils sont dits « indépendants »). Cette variable correspond donc à une échelle nominale à deux modalités équiprobables (elles ont autant de chances l’une que l’autre d’être choisies).
On peut facilement dénombrer les probabilités d’obtenir un résultat quand le nombre de tirages est réduit. Ici, on simule 3 tirages consécutifs qui ont autant de chances d’aboutir à un succès ou un échec (ou pile ou face, blanc ou noir, en rebond ou non, satisfait ou pas, etc.) :
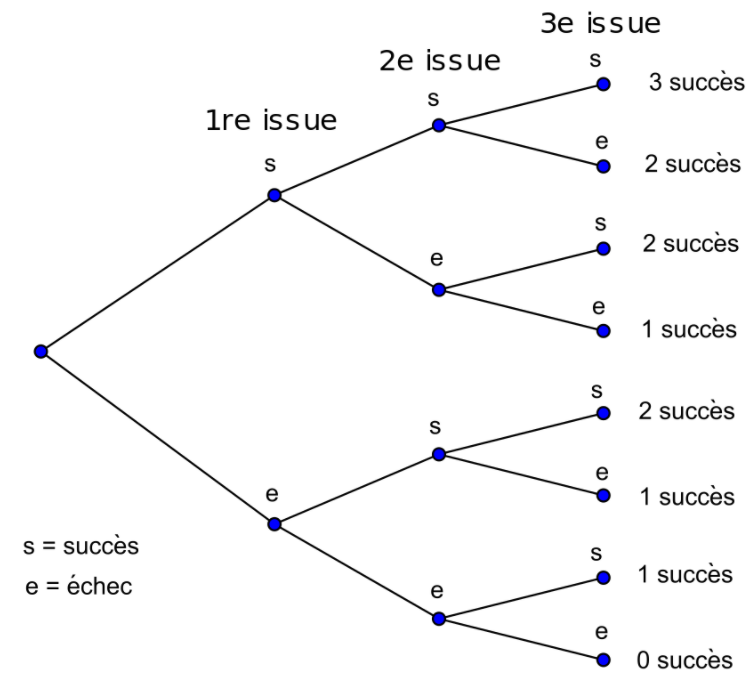
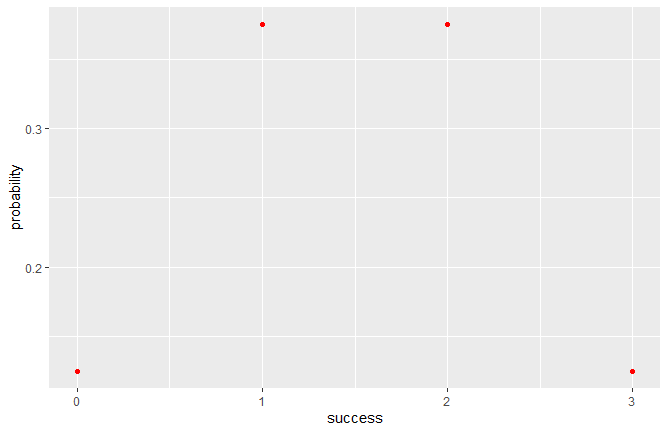
On constate qu’il n’y a qu’1 chance sur 8 (12,5 %) de n’avoir aucun succès. De même que pour un tirage ne donnant que des succès. Par contre, il y a 3 chances sur 8 (37,5 %) d’obtenir 2 succès et 1 échec ou l’inverse. Graphiquement, cela s’affiche comme ci-dessous. On appelle cela une fonction de masse :
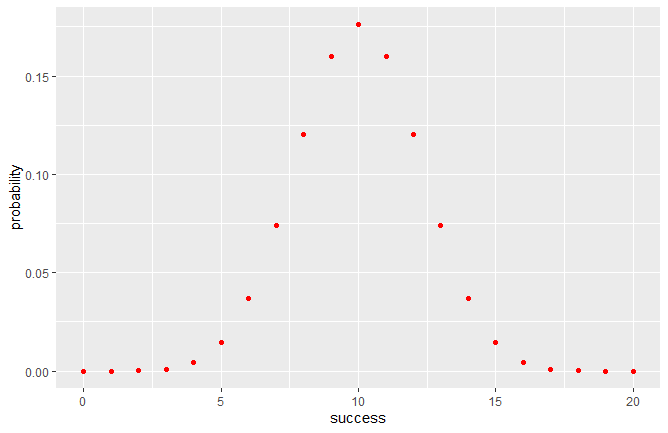
Dénombrer à la main les probabilités d’apparition de tirages aléatoires devient très vite fastidieux lorsque leur nombre augmente. Heureusement, la loi binomiale nous permet de le faire facilement, et des logiciels de statistiques tels que R permettent de la calculer simplement. Ainsi, grâce à la loi binomiale, on peut étendre l’exercice à 20 tirages équiprobables :
Et même 40 tirages :
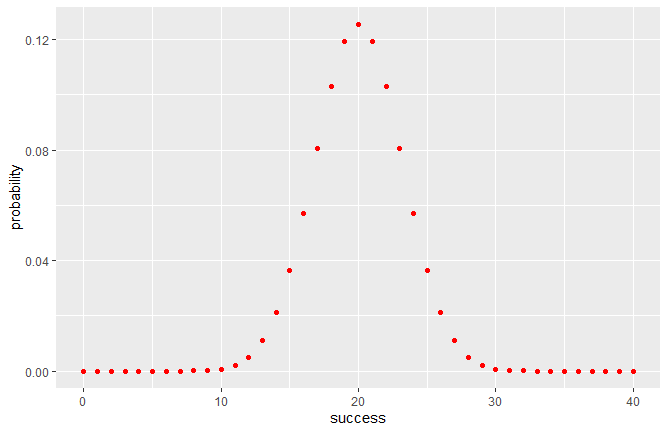
On se rend compte que les probabilités d’avoir telle ou telle répartition des tirages (c’est-à-dire la proportion de pile et de face) tendent à prendre une forme de cloche caractéristique (nous reviendrons sur ce point).
Si ce résultat peut sembler contre-intuitif, on peut s’en convaincre de façon empirique en utilisant une « planche de Galton ». Ce dispositif mécanique simule la chute d’un grand nombre de billes sur des plots les faisant passer aléatoirement à gauche ou à droite (ce qui correspond à autant de pile ou face).
L’expérience confirme bien les prévisions mathématiques. Mais, comment cette distribution de probabilités peut-elle nous être utile dans la mesure de l’expérience utilisateur et de la performance digitale ?
Appliquer les probabilités à la mesure du trafic d’un site web
Revenons aux données que nous avons présentées dans l’article consacré à la compréhension des erreurs de mesures. Nous y évoquions la part d’hommes et de femmes consultant UXMetric. C’est une variable aléatoire à deux modalités : nous ne connaissons pas la conjonction des causes conduisant des hommes ou des femmes à consulter ce site. Nous reproduisons ci-dessous, les proportions respectives d’hommes et de femmes ayant consulté notre site, à 2 périodes consécutives :
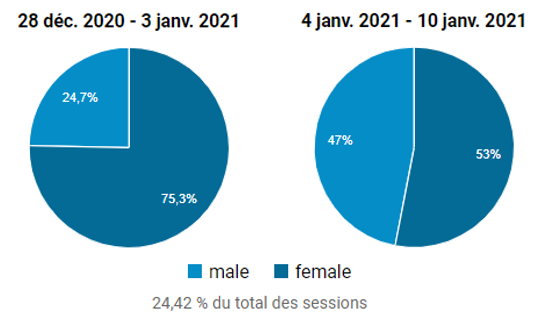
On constate que d’une semaine à l’autre, la proportion d’hommes et de femmes visitant le site a varié d’à peu près 25-75% à 50-50% (selon Google Analytics, nous négligeons volontairement les biais de collecte d’informations de cet outil). La question est de savoir quelle est la probabilité d’observer ces proportions alors que l’on ne connait pas a priori la répartition par genre de nos visiteurs. Sachant que sur cette période, il y avait à peu près 130 visiteurs hebdomadaires, mais que Google Analytics a échantillonné 24,42% des sessions (soit 33 sur 130), on trace les lois binomiales suivantes : l’une équiprobable (50% d’hommes ou de femmes), l’autre biaisée (25% de femmes pour 75% d’hommes) :
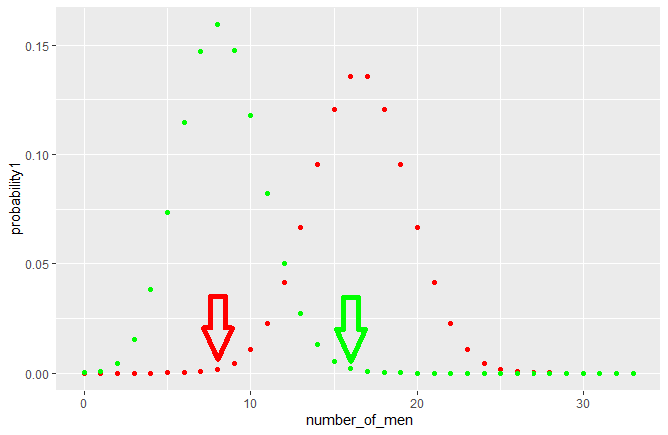
On constate que si l’audience d’UXMetric est effectivement composée de 25% d’hommes pour 75% de femmes (distribution verte), il n’est pas impossible, bien que peu probable, en échantillonnant aléatoirement 24,42% des sessions sur 130, d’obtenir 50% d’hommes et de femmes (flèche verte). Réciproquement, si notre audience contient autant d’hommes que de femmes (distribution rouge), il n’est pas exclu que l’échantillonnage prélève seulement 25% d’hommes pour 75% de femmes (flèche rouge). Il est bien sûr possible qu’une cause qui nous est inconnue explique cela, mais tant qu’elle n’est pas identifiée, on ne peut pas la différencier du hasard. Cela peut néanmoins nous alerter sur un possible biais. Auquel cas, il nous appartiendrait de déterminer quelle pourrait en être la cause.
Nous n’avons cependant aucune raison de penser que la répartition par genre des visiteurs de notre site ne soit pas équilibrée. Et c’est bien ce qu’indique un échantillonnage de 39,45% des 12000 sessions totales depuis la création du site (au 01/02/2021) :
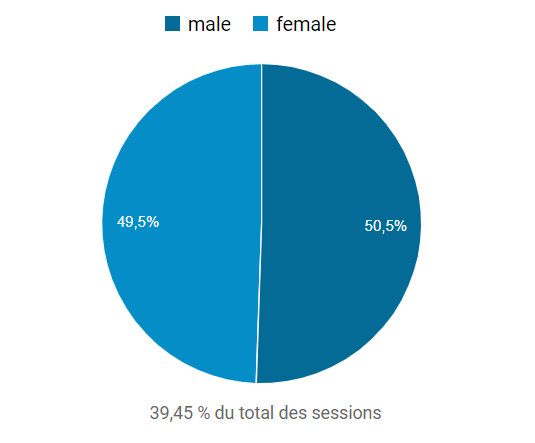
Comme le montre le graphique suivant, la probabilité qu’il en soit autrement, même en échantillonnant 39,45% des 12000 sessions, est vraiment infime (bien que toutefois possible) :
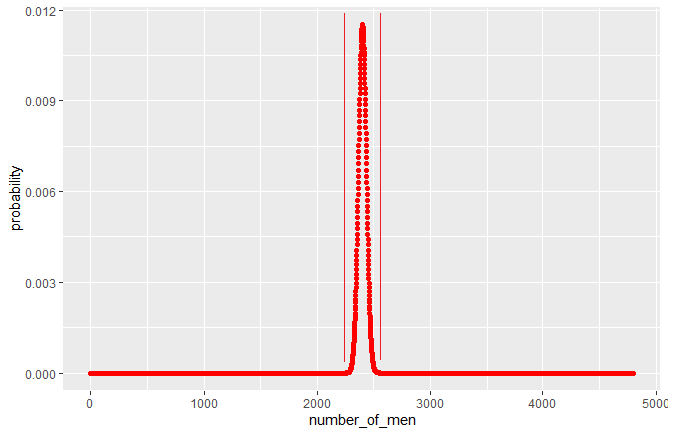
Les probabilités les plus élevées se massent autour de la valeur cible, à savoir 50% d’hommes ou de femmes. Bref, la “cloche” devient plus étroite. Les proportions qui s’éloignent du 50-50, si elles ne sont théoriquement pas nulles, sont si proches de zéro qu’elles sont en réalité quasi-impossibles à obtenir sur un échantillon de cette taille. Mais pas sur un plus petit échantillon de “seulement” 33 observations.
Des pièces aux dés…
Comment ce raisonnement s’applique-t-il lorsque le hasard s’exerce sur une variable à plus de deux modalités ? Il suffit de remplacer la pièce par un dé ! Le principe reste le même, et correspond donc à une variable aléatoire nominale ou ordinale à N modalités. Bien qu’il existe toutes sortes de dés, contentons-nous pour l’exemple d’un dé à 6 faces équiprobables (donc non pipé) que l’on va lancer de 1 à 5 fois (comme le montre la figure 9). Dans ce cas, la loi binomiale est remplacée par la loi multinomiale. Celle-ci est en réalité assez difficile à représenter graphiquement, c’est pourquoi, par commodité, on va additionner les résultats obtenus à chaque jet.
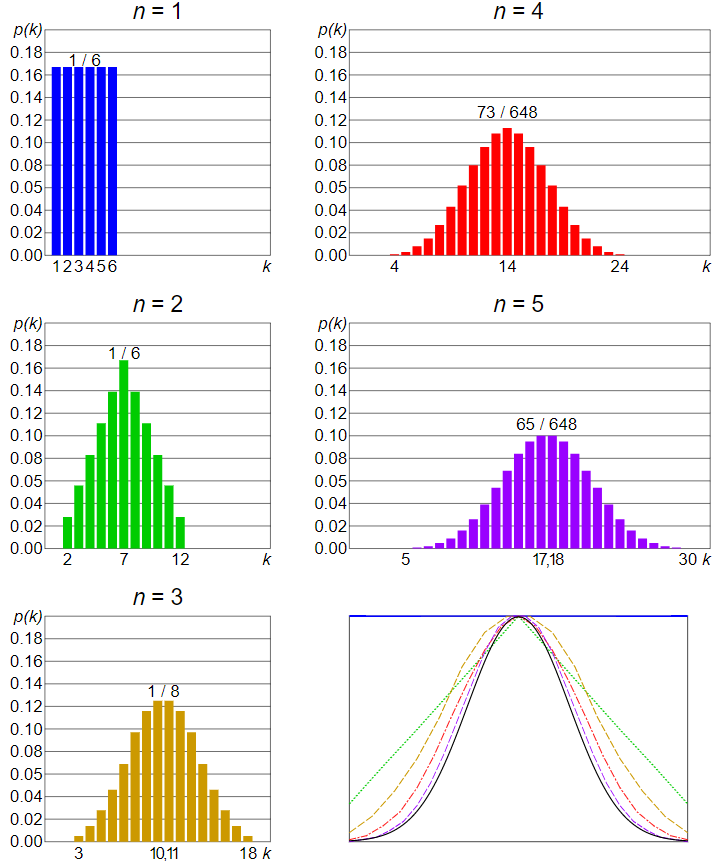
Lorsqu’on lance le dé une fois, il y a 1 chance sur 6 de tomber sur l’une ou l’autre des faces (graphique bleu pour N=1 lancé). Si on lance le dé 2 fois et qu’on additionne les résultats obtenus, on obtient le graphique vert (N=2). Sur 36 combinaisons possibles (6×6 faces), une seule combinaison peut donner 2 (1+1) ou 12 (6+6). Par contre, 6+1, 1+6, 5+2, 2+5, 4+3 et 3+4 peuvent donner 7. Soit 6 chances sur 36, donc 1 sur 6. Si l’on augmente le nombre de jets du dé, on constate que la probabilité d’obtenir telle ou telle somme prend là encore cette forme de cloche déjà observée : c’est ce que l’on appelle une distribution normale.
On l’appelle ainsi car le théorème central limite prédit que toute variable aléatoire (ou presque) tend vers cette distribution lorsque le nombre de tirages devient important (et que ceux-ci sont indépendants les uns des autres, c’est-à-dire que les tirages précédents n’influencent pas les suivants). C’est ce qu’illustre le dernier graphique en bas à droite, qui juxtapose les différentes distributions calculées pour 2 à 5 lancés (correspondant aux couleurs des graphiques), et la distribution normale (en noir). On voit bien cette convergence au fur et à mesure que le nombre de jets augmente.
Cela justifie l’importance de la loi normale dans les statistiques traditionnelles.
… Des dés aux boules !
Cependant, la loi normale ne s’applique qu’à des variables continues, ce qui n’est pas le cas des pièces ou des dés, correspondant eux à des variables discrètes. Elles ne peuvent pas prendre une infinité de modalités, comme les échelles continues. Pourtant, le raisonnement reste le même. S’il existe des dés à 3, 4, 6, 10, 30, 50 ou même 120 faces, que pourrait être un dé avec une infinité de faces ? Une boule ! C’est ce qui se passe lorsque l’on mesure une variable qui peut prendre une infinité de valeurs.
C’est le cas par exemple du temps de chargement d’UXMetric.com, que l’on a mesuré 90 fois avec l’outil webpagetest.org.
Le problème est que si la boule est constituée d’une infinité de faces, la probabilité de tomber sur l’une ou l’autre est de 1 sur l’infini ! Ce qui équivaut à zéro. C’est assez contre intuitif. Regardons comment se répartissent les 90 mesures de temps de chargement que nous avons collectées :
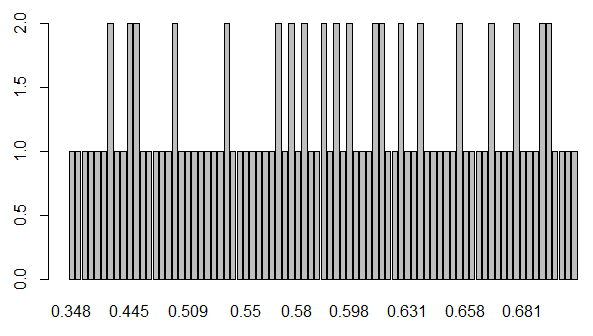
Comme il y a théoriquement une infinité de durées de chargement possibles, on n’observe en général chaque mesure qu’une seule fois. Restent quelques durées mesurées 2 fois. C’est évidemment lié à la précision de l’outil de mesure qui ne descend pas sous le millième de seconde (alors que les durées de chargement réelles le peuvent). Par conséquent, ce graphique en forme de peigne nous montre que toutes les durées de chargement possibles ont toutes la même probabilité d’être mesurées. C’est une particularité propre aux échelles continues.
Pour dépasser ce problème, on ne va plus chercher à déterminer la probabilité (ou fréquence) d’apparition d’une valeur précise, mais d’un ensemble de valeurs contiguës : C’est ce que l’on appelle une “classe”. Cela revient à discrétiser la variable continue. La classe contenant l’effectif le plus élevé est alors appelée classe “modale”. Elle se comporte alors comme une variable ordinale. Graphiquement, cela se présente ainsi :
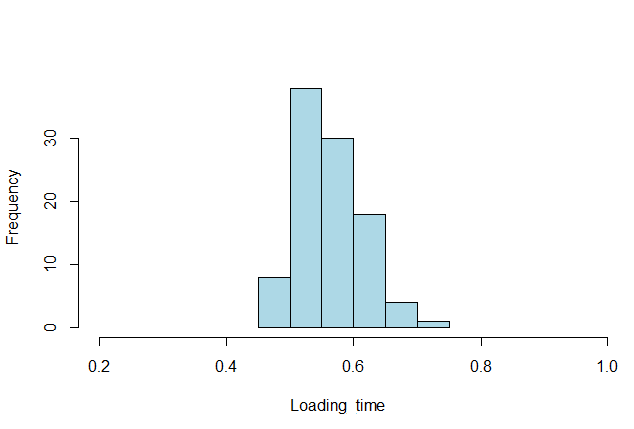
Contrairement aux distributions précédentes que nous avons représentées graphiquement et qui étaient théoriques, celle-ci est empirique. C’est pourquoi elle représente des fréquences (observées) plutôt que des probabilités (attendues).
La question est de savoir à quoi ressemblerait cette distribution si elle avait une infinité de classes. Bref, comme si elle était continue, ce qu’elle est ! Pour cela, il faut passer de la notion de probabilité à celle de “densité de probabilité”, représentée ainsi :
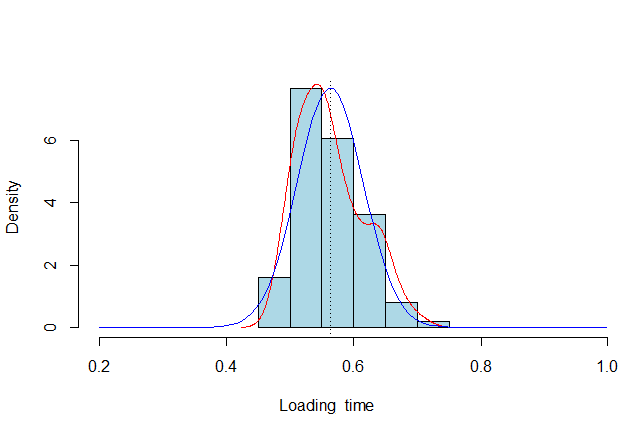
On constate que la densité de probabilité observée s’écarte sensiblement de la distribution normale théorique. Si c’est vrai aussi bien en termes de forme que de moyenne, elle n’en est pourtant pas si éloignée. On retrouve effectivement cette forme de “cloche”, mais imparfaite. La forme de cloche se dessine mieux sur la droite de la distribution que sur la gauche. C’est tout-à-fait normal lorsque l’on mesure une durée. La loi normale se distribue théoriquement de moins l’infini à plus l’infini. Or, ici, l’échelle de mesure dispose d’une borne à gauche. On ne peut pas mesurer des durées inférieures à zéro. C’est ce qui explique cette asymétrie.
Au final, l’intérêt de ce type de représentation est de pouvoir déterminer à quelle point une mesure est atypique, à quel point elle s’éloigne de la moyenne (qui est la valeur attendue si l’on répète plusieurs fois la mesure, ce que l’on appelle l’espérance mathématique). Car plus une mesure s’éloigne de la moyenne et plus elle devrait être rare. Cela permet d’évaluer l’incertitude liée aux aléas de mesure et d’échantillonnage.
Conclusion
L’objectif de cet article était de sensibiliser à la prise en compte des facteurs aléatoires. Ils influencent les mesures que l’on peut faire en matière d’expérience utilisateur et de performance digitale. L’idée est de prendre du recul vis-à-vis de l’analyse que l’on fait des métriques pour améliorer nos interprétations. Dans cette optique, nous vous invitons à visionner la vidéo ci-dessous de Mickaël Launay. Elle explique comment mieux se représenter le “hasard” et comment il agit :
