
Dans un précédent article, nous avons défendu l’idée que le meilleur indicateur de la qualité de l’expérience utilisateur d’un service était son utilisation effective. Evidemment, cela implique de connaitre le nombre total d’utilisateurs potentiels de ce service, sans quoi cette métrique n’a aucun sens. Cela n’est pas si évident, et bien souvent, c’est tout simplement impossible. Pourtant, il est possible de comparer le nombre personnes vivant une expérience à un moment donné à ce nombre à un moment précédent. On peut ainsi dégager une tendance dans l’évolution de l’usage du service.
Si l’on peut utiliser cette tendance pour prévoir quel sera le nombre d’utilisateurs ultérieurement, cela ne renvoie à rien de moins que de prédire l’avenir ! Ceci grâce à une méthode statistique aisément disponible et facile à mettre en oeuvre. Nous allons bien sûr vous expliquer comment.
Contexte
Les données que nous allons utiliser pour illustrer notre démarche sont des données réelles. Elles sont issues de log d’un éditeur de logiciel Saas (Software as a service, en ligne) de marketing relationnel collectées à propos de l’adoption d’une nouvelle fonctionnalité intégrée à cette application :
| Mois | Mai | Juin | Juillet | Août | Septembre | Octobre |
| Nbre d'utilisateurs | 76 | 114 | 122 | 140 | 148 | 158 |
Ce tableau présente le nombre d’utilisateurs par mois de cette fonctionnalité de mai à octobre.
Pourquoi prédire l’adoption d’un service ?
L’industrie du digital est un secteur jeune, concurrentiel, et en plein essor. Il est parfois difficile d’avoir le recul nécessaire à prendre les bonnes décisions pour orienter les évolutions des produits et services sur lesquels on travaille. C’est tout l’intérêt d’adopter une démarche de data-driven. C’est une approche assez classique de business intelligence.
L’enjeu va consister ici à avoir un temps d’avance pour la prise de décision en anticipant la valeur que va prendre un KPI (key performance indicator, indicateur clé de performance). En l’occurrence, pour évaluer l’adoption d’un service sur les prochaines semaines, le KPI est ici le nombre d’utilisateurs par mois. Attention cependant ! cette prévision n’est pas une prédiction, et des éléments nouveaux non pris en compte peuvent invalider l’anticipation réalisée.
Comment cela fonctionne-t-il ?
C’est très simple. Par commodité, nous allons utiliser l’outil Google Sheets, mais cela fonctionne à peu près de la même façon avec n’importe quel tableur, comme par exemple Microsoft Excel.
Pour commencer, nous transformons l’échelle temporelle pour la rendre continue, et convertissons les mois en jours. Nous y ajoutons également un “temps zéro” pour faciliter la compréhension, mais le principe reste identique, les données d’usage sont collectées tous les mois (ou tous les 30 jours) :
| Nbre de jours | 0 | 31 | 61 | 92 | 123 | 153 | 184 |
| Nbre d'utilisateurs | 0 | 76 | 114 | 122 | 140 | 148 | 158 |
L’idée est la suivante : prédire pour chaque période de 30/31 jours à venir (donc pour chaque mois) le nombre de personnes qui utiliseront la nouvelle fonctionnalité à partir des données précédentes. Pour ce faire, nous allons utiliser la fonction courbe de tendance (trendline) de Google sheets. Il faut attendre d’avoir 3 observations (donc 2 mois de recul dans notre exemple, sachant qu’à t=0, il n’y a pas encore d’utilisateur puisque la fonctionnalité vient d’être implémentée) pour dégager une première tendance. En effet, si l’on se contentait de seulement 2 observations, on ne pourrait pas déterminer la forme de la courbe de tendance.
Bien que seront évoqués (mais pas développés) certains aspects mathématiques de la démarche (pour justifier notre méthode), aucune connaissance mathématique n’est requise pour comprendre la démarche. Tout est expliqué de façon à ce que vous puissiez reproduire notre exemple, y compris sur vos données.
Phase 1 : Affichage du graphique à partir des données
La première étape consiste à sélectionner la plage de données et d’insérer le graphique correspondant (liseré rouge sur la capture d’écran) :
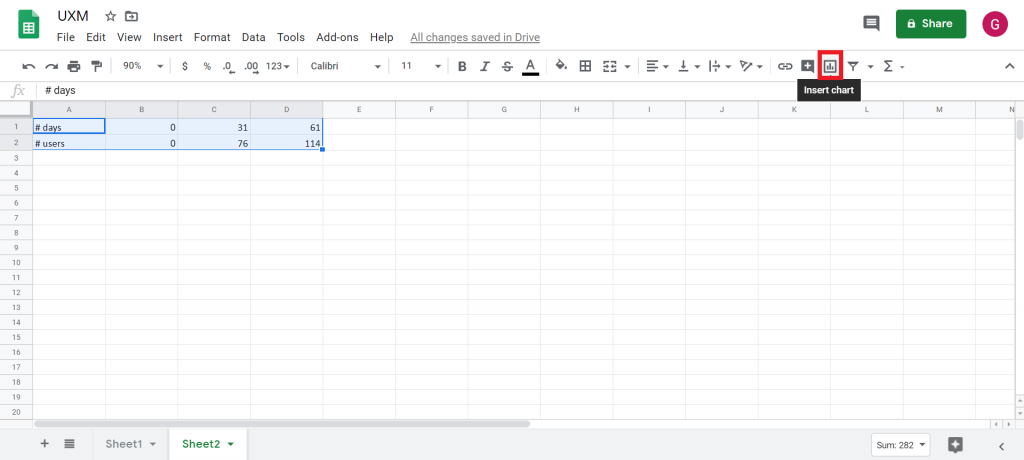
Un graphique par défaut apparaît, mais ce n’est pas celui que nous voulons. Dans l’onglet Setup , on ouvre le menu déroulant Chart type, il faut choisir Line chart.
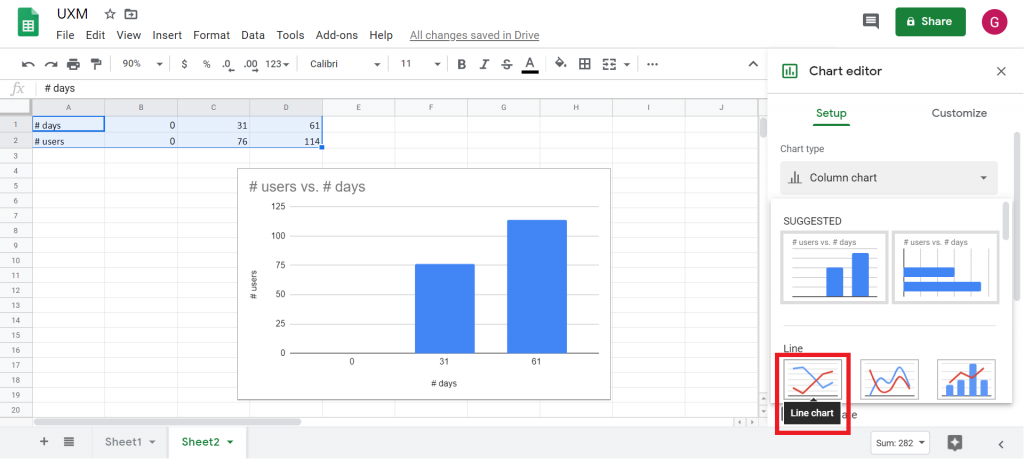
Phase 2 : Affichage de la courbe de tendance et des informations associées
On obtient un graphique dont les points sont reliés par des segments de droite. A partir de là, il faut afficher l’onglet Customize et ouvrir le volet Series :
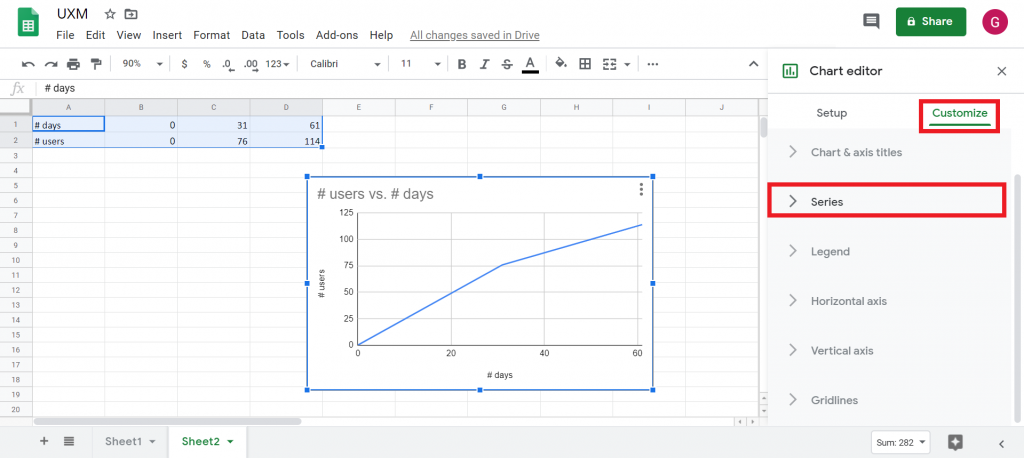
On y sélectionne tout d’abord Trendline (affichage de la courbe de tendance en bleu clair) et Show R². Ce dernier point mérite quelques explications.
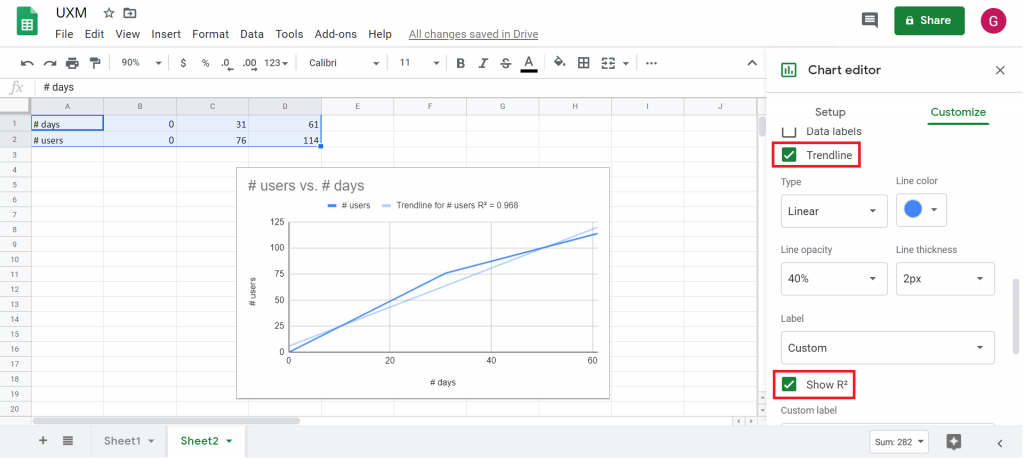
Le R² ou coefficient de détermination est un indicateur de l’adéquation de la courbe de tendance avec nos données. Il est théoriquement compris entre 0 et 1. Plus il est élevé, et donc, proche de 1, plus la courbe de tendance est ajustée aux données. Formulé autrement, quand R²=1, alors la courbe de tendance passe exactement par tous les points (ou nœuds) correspondant aux données. Plus la courbe s’éloigne de ces points et plus le R² diminue.
La formule de calcul du R² est assez complexe, et renvoie à des concepts statistiques (corrélation & régression) que nous n’aborderons pas ici. Le R² correspond en fait au coefficient de corrélation linéaire élevé au carré. Ce coefficient mesure l’intensité de la relation linéaire entre une variable explicative (en abscisse, ici le temps) et une variable à prédire (en ordonnée, le nombre d’utilisateurs). C’est pourquoi le coefficient de détermination devrait être réservé aux seules relations linéaires, c’est-à-dire quand la courbe de tendance qui résume le nuage de points est une droite d’équation y = Ax + B.
Cependant, la relation n’est pas forcément “linéaire”, et la courbe de tendance n’est pas nécessairement rectiligne. Elle peut prendre différentes formes, comme nous allons le voir. Malgré cela, nous continuerons à utiliser le coefficient de détermination, même si les fondements mathématiques qui permettent son calcul ne sont théoriquement plus valables dans le cadre d’une relation non linéaire (cette approximation peut conduire au calcul d’un R²>1, ce qui est impossible). Pour autant, et en dépit de cette approximation, cette valeur reste fort utile, y compris dans le cas de relation non linéaire.
Phase 3 : Choix de la courbe de tendance et affichage de l’équation correspondante
Plusieurs types de courbes de tendances sont disponibles. Pour commencer, affichons l’équation de la courbe de tendance avec le menu déroulant Label pour lequel on choisit l’item Use equation. Elle apparaît au-dessus du graphique, à gauche du R², et nous sera utile par la suite.
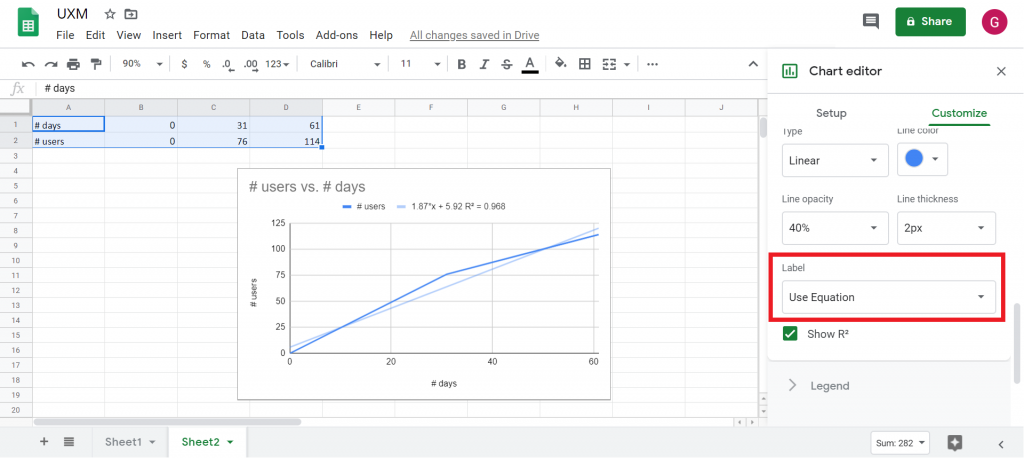
Sélectionnons maintenant parmi les différents types de courbes celle qui va être le plus adaptée à résumer (et donc prédire) nos données :
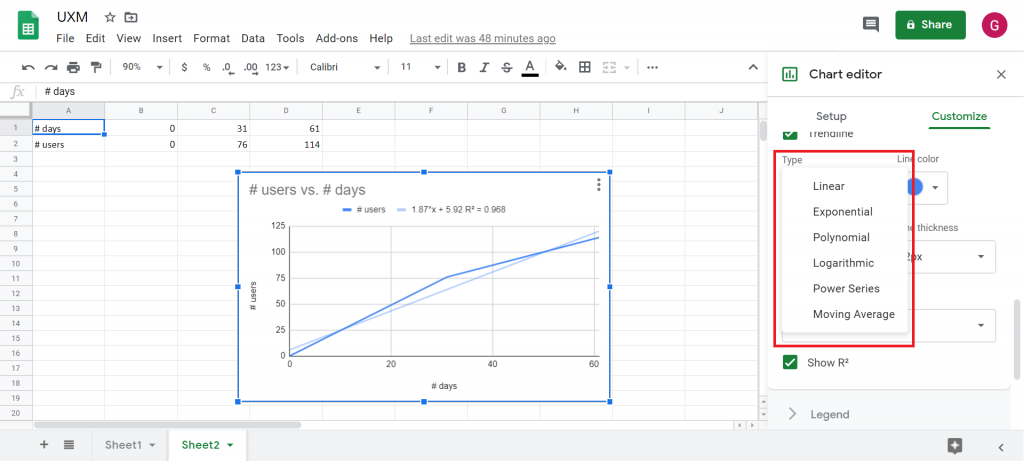
Six courbes de tendances sont disponibles dans Google sheets (mais il en existe d’autres). Pour chacune de ces courbes, on indique le type d’équation qui les décrivent. La variable x représente l’axe des abscisses, c’est le prédicteur, alors que la variable y (axe des ordonnées) est la variable à prédire. Les autres lettres (a, b, … z) représentent des paramètres qui seront déterminés automatiquement par Google sheet (méthode des moindres carrés) :
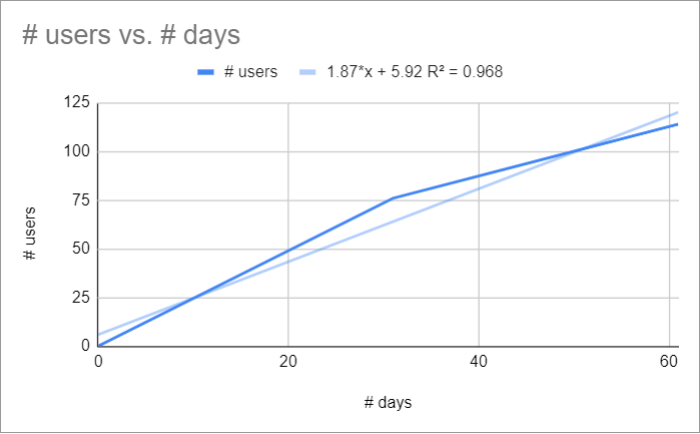
- Linéaire : Pour les données qui suivent de près une ligne droite.
Équation de la courbe de tendance : y = ax+b.
Il s’agit de l’exemple que nous avons utilisé par défaut jusque-là :
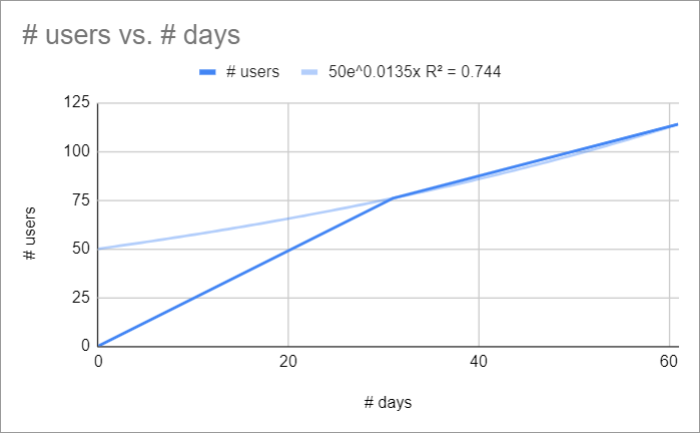
- Exponentielle : Pour les données qui augmentent et diminuent proportionnellement à leur valeur actuelle.
Équation : y = a*e^(bx).
On constate qu’elle s’ajuste moins bien à nos données, ce qui se voit à la lecture du R² qui chute à 0.744 (contre 0.968 pour la courbe linéaire).
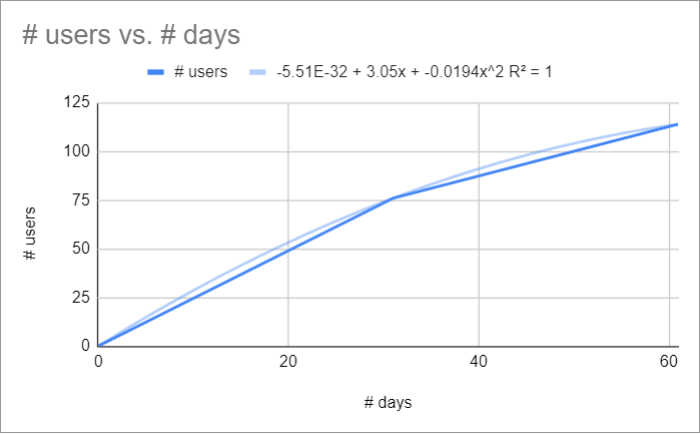
- Polynôme : Pour les données qui varient.
L’équation de la tendance prend alors la forme suivante : ax^n + bx^(n-1) + … + zx^0.
Ce type de courbe peut simuler des tendances à la hausse et à la baisse qui se succèdent.
On notera que dans ce cas, le R² = 1, ce qui témoigne d’un ajustement parfait !
Attention à ce “miracle” en trompe-l’œil. Les polynômes dit de Lagrange peuvent interpoler parfaitement une série de points sans pour autant en représenter la tendance (phénomène de Runge). Ainsi, l’adéquation de la courbe aux données peut n’être d’aucune utilité pour prédire les données futures.
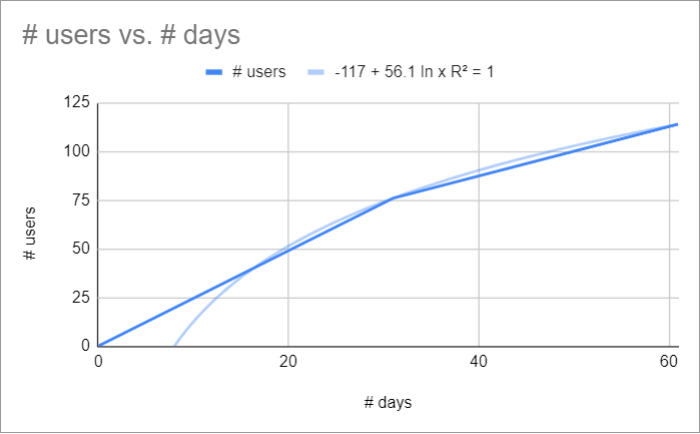
- Logarithmique : Pour les données qui augmentent ou diminuent rapidement puis s’aplatissent.
Équation de la courbe : y = a*ln(x) + b.
Ici aussi, R² = 1, mais l’ajustement de cette fonction aux données est moins systématique qu’une courbe polynomiale, ce qui est de bon augure.
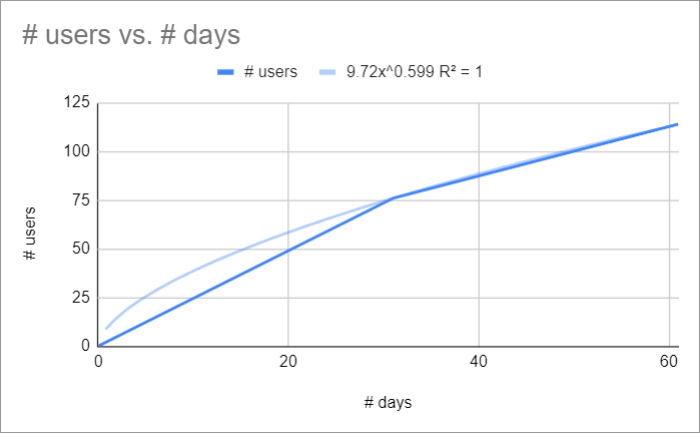
- Série de puissance : Pour les données qui augmentent ou diminuent proportionnellement à leur valeur actuelle au même rythme.
Équation de la courbe : y = a*x^b.
Les remarques précédentes sur le R² restent valables dans le cas présent.
- Moyenne mobile : Aide à lisser les données qui sont instables ou plus changeantes. Nous ne traiterons pas ici cette dernière possibilité car elle ne permet pas d’afficher l’équation de la courbe et de calculer le R².
Pour choisir la courbe de tendance la mieux ajustée aux données, il est illusoire de ne tenir compte que du R². En effet, celui-ci ne mesure que la qualité mathématique de l’ajustement. Cependant, pour un faible nombre de données (comme c’est le cas ici), plusieurs modèles peuvent s’ajuster parfaitement.
Le choix du modèle doit se faire en premier lieu sur des considérations théoriques ou à partir de connaissances empiriques. Nos données reflètent l’utilisation d’une nouvelle fonctionnalité implémentée à un logiciel Saas. Nous avons des raisons de penser que si beaucoup d’utilisateurs vont constater cette nouveauté peu de temps après son intégration, le nombre de nouveaux utilisateurs va s’amenuiser au fil du temps. C’est donc le modèle logarithmique qui nous semble le plus adapté.
Phase 4 : Utiliser l’équation de la courbe de tendance pour prédire les valeurs à venir
En se reportant au graphique 4 représentant la courbe de tendance logarithmique, on récupère son équation :
y= -117 + 56,1 ln X.
Formulé autrement, elle revient à écrire que :
Nbre d’utilisateurs = -117 + 56,1 ln (Nbre de jours).
Nous pouvons donc utiliser cette formule pour prévoir le nombre d’utilisateurs à 92 jours. Il suffit de copier coller dans Google l’équation et d’en remplacer la valeur x (nombre de jours) par la valeur pour laquelle nous voulons prédire le nombre d’utilisateurs :
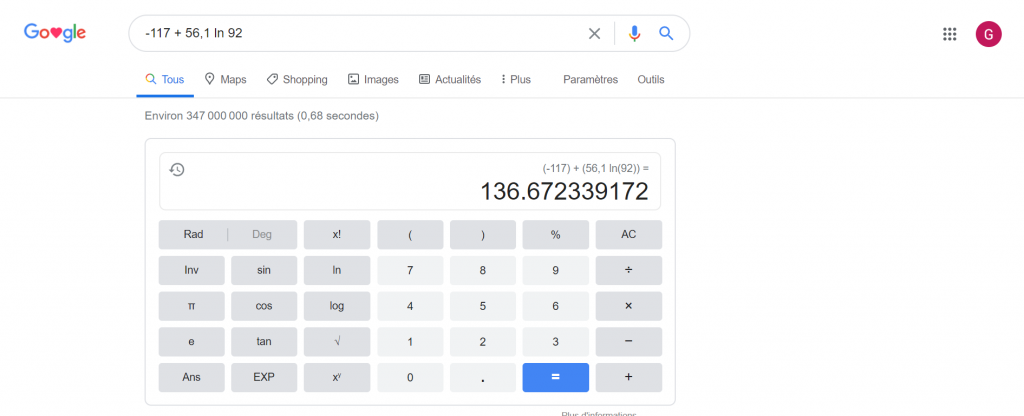
Cela nous donne (à peu près) 136 utilisateurs, à comparer aux 122 effectivement constatés. Cela représente une erreur de 136/122≅1,114, soit 11,4% d’erreur. C’est pas mal, mais on peut sans doute mieux faire avec cette nouvelle donnée pour prédire le nombre d’utilisateurs du mois suivant :
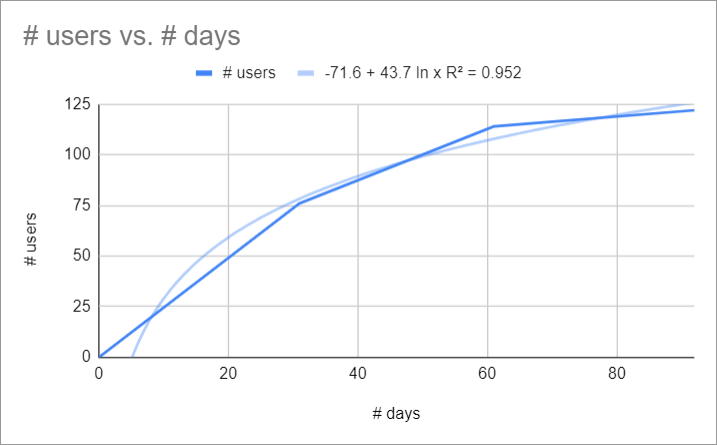
On récupère la nouvelle équation générée Nbre d’utilisateurs = -71,6 + 43,7 ln (Nbre de jours) pour prédire le nombre d’utilisateurs à 122 jours. On obtient 138 au lieu de 140, soit 1,4% d’erreur.
C’est mieux ! Le tableau suivant recense toutes les valeurs obtenues pour chaque mois à partir des informations précédentes :
| Nbre de jours | 0 | 31 | 61 | 92 | 122 | 153 | 183 |
| Nbre d'utilisateurs | 0 | 76 | 114 | 122 | 140 | 148 | 158 |
| Nbre d'utilisateurs prévus | NA | NA | NA | 136 | 138 | 149 | 157 |
| Taux d'erreur | NA | NA | NA | 11,4% | 1,4% | 0,6% | 0,6% |
| R2 | NA | NA | NA | 1 | 0,952 | 0,973 | 0,981 |
Conclusion
On ne peut que constater la précision des prévisions dans le cadre de notre exemple : moins de 1% d’erreur au bout de seulement 5 mois ! On remarque également que l’ajustement du modèle n’est pas complètement lié à la qualité de la prévision. Lorsqu’il y a peu de données, le modèle peut être parfaitement ajusté (R²=1) et moins explicatif qu’un modèle moins bien ajusté, mais prenant en compte plus de données. Cela illustre l’importance de bien choisir le type de courbe et ne pas se focaliser sur le seul R².
Dans cet exemple, nous nous sommes cantonnés à prédire le nombre d’utilisateurs pour les 30 jours à venir. Il est bien sûr possible de faire une prédiction à plus long terme (60, 90 ou 120 jours). Cependant, le risque d’erreur devient nettement plus important, même avec un modèle très ajusté. Comme pour la météo, il est plus facile de prévoir le temps du lendemain que celui qu’il fera dans 3 mois.
Cette méthode n’est pas assimilable aux méthodes statistiques traditionnelles de régression, dont les enjeux diffèrent. Il ne s’agit pas ici, à partir de données recueillies sur un échantillon, d’inférer les propriétés constatés sur celui-ci à la population dont il a été extrait. Il ne s’agit pas non plus d’apprentissage automatique (machine learning) dans le sens où les méthodes de prédictions de variables quantitatives ne résolvent pas des problèmes de classification (prédiction de variables catégorielles).
Quoi qu’il en soit, cette méthode assez simple à mettre en oeuvre peut aisément venir compléter la boite à outils des UX designers et de tout autre consultant s’intéressant à la performance digitale.
